트리에서 내부마디(internal node)는 최소한 하나의 자식마디를 가진 마디를 말한다.
2. 잎마디는 모두 깊이가 d이다.
1. d-1의 깊이까지는 완전한 이진 트리이다.
2. 깊이가 d인 마디는 모두 왼쪽 끝으로 모여 있다.
실질적으로 완전한 이진 트리는 정의하기 어렵지만, 그림으로 그 특징을 파악하기는 쉽다. 다음의 트리가 실질적으로 완전한 이진 트리이다.

이제 힙(heap)을 정의해 보자. 힙은 다음을 만족하는 실질적으로 완전한 이진 트리이다.
1. 마디에 저장된 값은 순서가능집합(ordered set: 순서를 매길 수 있는 원소로 구성된 집합)
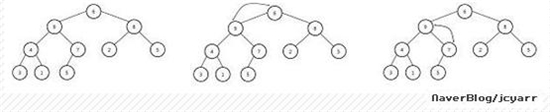
{ // 실행 전: 뿌리마디를 제외한 H의
node parent, largechild; // 모든 마디들은 힙 성질을 만족한다.
// 실행 후: H는 힙이 된다.
parent = H의 뿌리마디;
largerchild = 큰 키를 가진 parent의 자식마디;
while (parent의 키가 largerchild의 키보다 작다){
parent = largerchild;
largerchild = 큰 키를 가진 parent의 자식마디;
}
}
{
keytype keyout;
바닥마디의 키를 뿌리마디로 옮김; // 바닥마디는 맨 오른쪽에 위치한 한 잎마디
바닥마디를 지움.
siftdown(H);
return keyout; // 힙 성질 회복
}
n개 키로 구성된 힙을 가지고, 키를 배열 S에 정렬된 순서로 위치시키는 의사코드는 다음과 같다.
void removekeys (int n, heap H, keytype S[])
{
index i;
for ( i = n; I >= 1; i--)
S[i] = root(H);
}
Heap정렬이 된 트리를 만드는 루틴은 다음과 같은 추상적 의사코드로 약술된 프로시저로 구현한다.
void makeheap (int n, heap& H) // H는 결국 힙이 됨.
{
index i;
heap Hsub; // Hsub는 결국 힙이 됨.
for (i = d - 1; i >= 0; i--) // 트리는 깊이가 d임.
for (깊이가 i인 모든 부분트리 Hsub)
siftdown(Hsub);
}
마지막으로, 힙정렬(Heapsort)을 하는 의사코드를 살펴보자(H에 실질적으로 완전한 이진 트리로 키는 이미 정돈되어 있다고 가정한다)
void heapsort (int n, heap H, keytype S[]) // H는 결국 힙이 됨.
{
makeheap (n, H);
removekeys (n, H, S);
}
위에서 제시된 코드를 적용하여 실질적으로 완전한 이진 트리에서 힙을 만드는 과정을
다음 그림이 보여준다.

(a) 초기상태 (b) 깊이가 d-1인 부분트리를 힙으로 만든다.
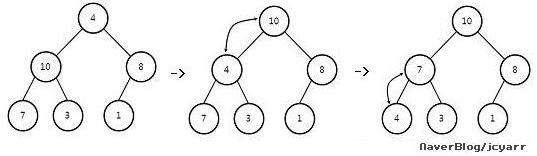
(c) 깊이가 d-2인 트리를 힙으로 만든다.
heap sort의 알고리즘은 다음과 같다.
알고리즘 1.1) Heap Sort ---------------------------------------------------------
* 문제 : 비내림차순으로 n개 키를 정렬
* 입력 : 양의 정수 n, 힙을 배열로 구현한 크기 n의 배열 H
* 출력 : 비내림차순으로 정렬된 키들로 구성된 배열 H.S
struct heap
{
keytype S[1..n]; // S의 인덱스는 1부터 n까지임.
int heapsize; // heapsize는 0부터 n사이의 값만 취함.
};
void heapsort ( int n, index& H)
{
makeheap (n, H);
removekeys (n, H, H.S);
}
void siftdown(heap& H, index I) // 레코드 대입의 횟수를 최소화하기 위해서
{ // 뿌리마디의 초기 키(siftkey)는 그 키의
index parent, largerchild; // 최종위치가 결정될 때까지 어떤 마디에도
keytype siftkey; // 할당되지 않는다.
bool spotfound;
siftkey = H.S[i];
parent = i;
spotfound = false;
while (2*parent <= H.heapsize && ! spotfound){
if (2*parent < H.heapsize && H.S[2*parent] < H.S.[2*parent +1])
largerchild = 2*parent + 1; // 오른쪽 자식마디의 인덱스는 부모마디의
else // 인덱스의 2배보다 1 더 많다.
largerchild = 2*parent; // 왼쪽 자식마디의 인덱스는 부모마디의
if (siftkey < H.S[largerchild]){ // 인덱스의 두 배이다.
H.S[parent] = H.S[largerchild];
parent = largerchild;
}
else
spotfound = true;
}
H.S[parent] = siftkey;
}
keytype root(heap& H)
{
keytype keyout;
keyout = H.S[1]; // 뿌리마디에서 키를 추출
H.S[1] = H.S[heapsize]; // 바닥마디의 키를 뿌리마디로 이동
H.heapsize = H.heapsize - 1; // 바닥마디를 지움.
Siftdown(H, 1); // 힙 성질 회복
return keyout;
}
void removekeys (int n, // 메모리를 절약하기 위해서
heap& H, // H는 주소로 전달됨
keytype S[]) // S의 인덱스는 1부터 n까지임.
{
index i;
for( i = n; i >= 1; i--)
S[i] = root(H);
}
void makeheap (int n, heap& H) // H는 결국 힙이 됨
{
index i; // n개 키가 배열 H.S에 있다고 가정
H.heapsize = n;
for(i = [n/2]; i >= 1; i--) // 깊이가 d-1인 자식마디를 가짐.
siftdown (H, i); // 마지막 마디는 배열의 [n/2]번째
}
'DS/ALGORITHUM' 카테고리의 다른 글
| POSTFIX (1) | 2008.06.20 |
|---|



